nx1.info | Creating a realtime Music Visualizer
What is digital music?
At the most fundemental level, a digital audio file is simply a series of numbers written in binary. We can see these numbers by using the python soundfile library (pip install soundfile). read_flac.py ------------import numpy as np
import soundfile as sf
file_path = 'Troya - Schizophrenic.flac'
data, sample_rate = sf.read(file_path)
print(f'Sample Rate = {sample_rate}')
for d in data:
print(d)
Output
------
Sample Rate = 44100
[ 0.00665283 -0.00546265]
[ 0.00637817 -0.00521851]
[ 0.00628662 -0.00494385]
[ 0.0065918 -0.00500488]
[ 0.00646973 -0.0050354 ]
[ 0.00643921 -0.00506592]
[ 0.00640869 -0.00509644]
[ 0.00628662 -0.00531006]
[ 0.0062561 -0.00558472]
[ 0.00613403 -0.00552368]
[ 0.00601196 -0.00561523]
[ 0.00582886 -0.00546265]
The left and right columns correspond to signal S(t) the normalized amplitudes (0 < S(t) < 1) of
the left and right speaker channels.
To decode the series, we require some key pieces of meta information, for my flac file these are:
- Sample Rate (f_s) = 44100 Hz
- Bits per Sample = 16 bits
- Bitrate (R) = 904 kbps
- Number of Channels = 2 Channels
Each sample in our flac file is made up of 16 bits, we can see how the bits are made up by converting
the decimal representation to binary.
to convert the signal float values to 16bit values we do
data = (data * (2**15)).astype(np.int16)
and to print the values and their binary representation we can change our print function to:
print(f'{d} {d[0]:016b} {d[1]:016b}')
This now outputs:
[ 218 -179] 0000000011011010 -000000010110011
[ 209 -171] 0000000011010001 -000000010101011
[ 206 -162] 0000000011001110 -000000010100010
[ 216 -164] 0000000011011000 -000000010100100
[ 212 -165] 0000000011010100 -000000010100101
[ 211 -166] 0000000011010011 -000000010100110
[ 210 -167] 0000000011010010 -000000010100111
[ 206 -174] 0000000011001110 -000000010101110
[ 205 -183] 0000000011001101 -000000010110111
[ 201 -181] 0000000011001001 -000000010110101
[ 197 -184] 0000000011000101 -000000010111000
[ 191 -179] 0000000010111111 -000000010110011
[ 185 -184] 0000000010111001 -000000010111000
[ 182 -185] 0000000010110110 -000000010111001
[ 184 -178] 0000000010111000 -000000010110010
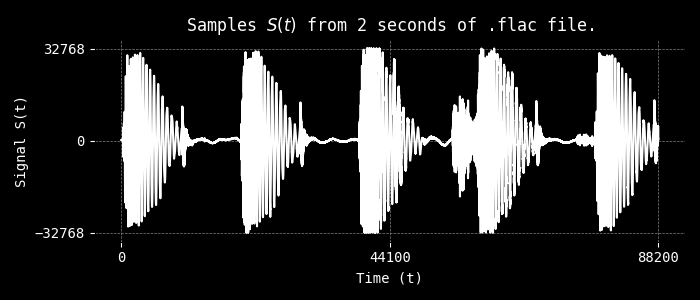
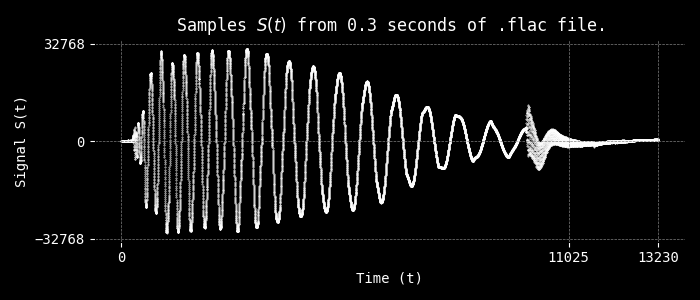
How can we process the stream of music?
Now we know what digital music is, we need to think about how we can use a continually ariving stream of numbers to drive some sort of visualization. The simplest visualization I can think of, is simply to print the value of the signal for every frame as the music plays. This involves to things 1. Playing the music, 2. printing the value.Streaming the Sample Data
Using pygame, we can have a loop that takes a chunk of samples and performs some operation on it. In this example I have calculated the fft and mean of a 2**15=32768 sized chunk of audio. Game runs at 60fps with a average frame time of 17ms. However since 2**15 samples turns out to be less than a second, so we probably would like to increase this. Running at 2**20=1,048,576 (~23secs) we begin to see the frame-rate drop below 60fps to 50 with our 400x400 output. 10^19 samples gives a average frametime of ~34ms, we'll use this for now. audio_streaming.py ------------------import numpy as np
import pygame, sys
from pygame.locals import *
import soundfile as sf
file_path = 'Troya - Schizophrenic.flac'
data, sample_rate = sf.read(file_path)
data_T = data.T
data_int16 = (data * (2**15)).astype(np.int16)
fft_chunksize = 2**15
pygame.init()
screen = pygame.display.set_mode((500, 400))
clock = pygame.time.Clock()
font = pygame.font.SysFont(name='consolas', size=15)
antialias = False
color = (255, 255, 255)
while True:
t = pygame.time.get_ticks()
mspf = clock.tick(60) # Miliseconds per frame
fps = clock.get_fps()
d = data_int16[t]
d_l, d_r = data_T[0], data_T[1]
chunk_start = t + 10
chunk_end = t + 10 + fft_chunksize
chunk = d_r[chunk_start:chunk_end]
fft = np.fft.fft(chunk)
fft_mean = np.mean(fft.real)
screen.fill((0, 0, 0))
screen.blit(font.render(f'{mspf}', antialias, color), (50,10))
screen.blit(font.render(f'{fps}', antialias, color), (50,30))
screen.blit(font.render(f'{t}', antialias, color), (50,50))
screen.blit(font.render(f'{d_l[t]:.2f} {d_r[t]:.2f}', antialias, color), (50,70))
screen.blit(font.render(f'{d[1]:016b}', antialias, color), (50,90))
screen.blit(font.render(f'{d[0]:016b}', antialias, color), (50,110))
screen.blit(font.render(f'{chunk_start} - {chunk_end} ({fft_chunksize})', antialias, color), (50,150))
screen.blit(font.render(f'{fft_mean:.2f}', antialias, color), (50,170+5*fft_mean))
v1 = abs(225 * fft_mean)
v2 = np.sin(v1)
pygame.draw.rect(screen, (255,v1,v1), [250, v1, v1, 50], 4)
pygame.display.update()